nLab nuclear matrix model
Context
Fields and quanta
fields and particles in particle physics
and in the standard model of particle physics:
matter field fermions (spinors, Dirac fields)
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
(also: antiparticles)
hadrons (bound states of the above quarks)
minimally extended supersymmetric standard model
bosinos:
dark matter candidates
Exotica
Duality in string theory
general mechanisms
-
electric-magnetic duality, Montonen-Olive duality, geometric Langlands duality
string-fivebrane duality
string-QFT duality
QFT-QFT duality:
-
effective QFT incarnations of open/closed string duality,
relating (super-)gravity to (super-)Yang-Mills theory:
-
Seiberg duality (swapping NS5-branes)
Contents
Idea
The nuclear matrix model (Hashimoto-Iizuka-Yi 10, Hashimoto-Matsuo-Morita 19) is a matrix model for baryons/nucleons in nuclear physics.
The model proceeds from the Witten-Sakai-Sugimoto model for QCD realized on intersecting D-branes, where baryons are embodied by wrapped D4-branes (“Witten’s baryon vertex”) on flavour D8-branes (D4-D8 brane bound states).
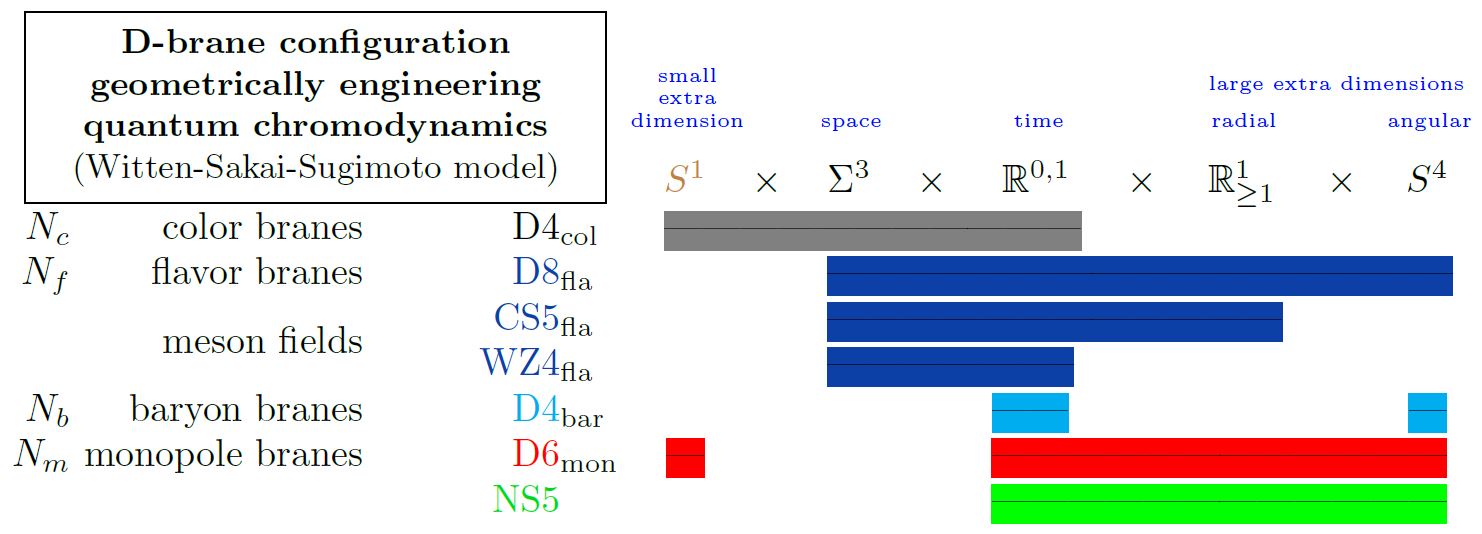
(graphics from Sati-Schreiber 19c)
Thus, encoding the D-brane dynamics of these D4-branes in a matrix model along the lines of the BFSS matrix model/BMN matrix model (for D0-branes) and the IKKT matrix model (for D(-1)-branes) leads to a matrix model for baryons and hence, potentially, for nucleons.
Related concepts
matrix models for brane dynamics:
| D-brane | matrix model |
|---|---|
| D0-brane | BFSS matrix model, BMN matrix model |
| D(-1)-brane | IKKT matrix model |
| D4-brane | nuclear matrix model |
| M-brane | matrix model |
|---|---|
| D2-brane | membrane matrix model |
See also:
References
Formulation of the model:
- Koji Hashimoto, Norihiro Iizuka, Piljin Yi, A Matrix Model for Baryons and Nuclear Forces, JHEP 1010:003, 2010 (arXiv:1003.4988)
Review:
- Sinya Aoki, Koji Hashimoto, Norihiro Iizuka, Matrix Theory for Baryons: An Overview of Holographic QCD for Nuclear Physics, Reports on Progress in Physics, Volume 76, Number 10 (arxiv:1203.5386)
Further development:
-
Si-wen Li, Tuo Jia, Matrix model and Holographic Baryons in the D0-D4 background, Phys. Rev. D 92, 046007 (2015) (arXiv:1506.00068)
-
Koji Hashimoto, Yoshinori Matsuo, Takeshi Morita, Nuclear states and spectra in holographic QCD, JHEP12 (2019) 001 (arXiv:1902.07444)
-
Yasuhiro Hayashi, Takahiro Ogino, Tadakatsu Sakai, Shigeki Sugimoto, Stringy excited baryons in holographic QCD, Prog Theor Exp Phys (2020) (arXiv:2001.01461)
Computation of nuclear binding energies in the model:
- Koji Hashimoto, Yoshinori Matsuo, Nuclear binding energy in holographic QCD (arXiv:2103.03563)
Created on March 8, 2021 at 05:45:12. See the history of this page for a list of all contributions to it.